第四章：熵和热力学第二定律

V. 相变

  1. 双相系统的自发演化 我们考虑一个Σ系统，它由一个纯物质组成，最初存在两个相1和2，其物质量分别为n1和n2（其中n = n1 + n2），并处于等温等压的单相单压状态下，压力为P，温度为T。提醒：平衡状态由最小的G确定。 稳定相对应于在给定的P和T下具有最低化学势。 两个相（具有任意的n1和n2）在化学势相等时处于平衡状态。这个条件意味着两个相之间的平衡是单变量的：如果T被固定，Peq = P(T)。

  2. 相变的熵 我们考虑同样的Σ系统，其中相1和相2是同一种纯物质的共存相。

  • 如果温度T被固定，相变从1到2的摩尔熵变为： ∆12𝑆𝑚 𝑇 = 𝑆𝑚2( 𝑇, Peq(T) ) - 𝑆𝑚1( 𝑇, Peq(T) )
  • 我们已经知道𝑆𝑚, gas > 𝑆𝑚, liquid > 𝑆𝑚, solid，因此有： ∆𝑣𝑎𝑝𝑆𝑚 𝑇 > 0，∆𝑓𝑢𝑠𝑆𝑚 𝑇 > 0和∆𝑠𝑢𝑏 𝑆𝑚 𝑇 > 0 它们的相反情况是：∆𝑙𝑖𝑞𝑆𝑚 𝑇 < 0，∆𝑠𝑜𝑙𝑆𝑚 𝑇 < 0和∆𝑐𝑜𝑛𝑑𝑆𝑚 𝑇 < 0
  • 与相变焓的关系：化学势的平衡可以写成以下形式：
  1. Clapeyron关系
  1. 推导 我们考虑相1和相2之间在接近温度T和T + dT的两个近邻平衡态。
  2. 结果 通常情况下，更为混乱的相较为稀薄：

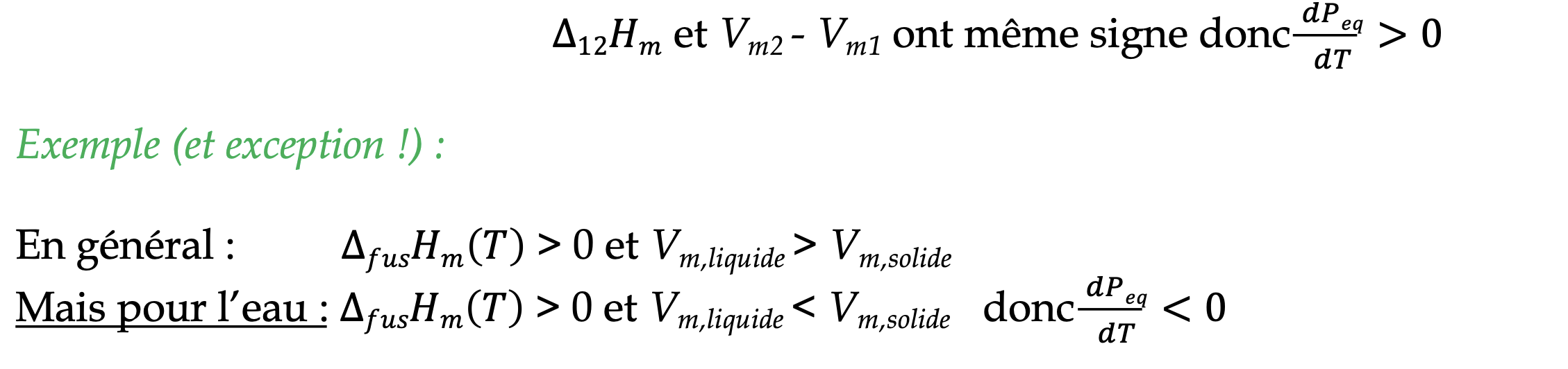
image-20231128214103234

  1. 液体-气体平衡的情况 • 实验：在这种情况下，平衡压力Peq被记作Psat（蒸汽饱和压力）。 • 初始系统：液态水，温度接近Teau = 80°C < 100°C = Tvap（P0 = 1 atm）。 • 使用泵降低压力。

• 观察：较大的减压使水沸腾。 假设在实验过程中Teau保持不变， 对于∆T = Teau - Tvap(P0 = 1 atm) < 0，我们得到∆𝑃𝑠𝑎𝑡 = 𝑃𝑠𝑎𝑡 (Teau ) - P0 < 0， 因此

• 我们知道： • 假设 ∆𝑣𝑎𝑝𝐻𝑚 𝑇 不依赖于温度，并且蒸汽是理想气体。 • 应用：在山上煮面的时间（对于水，∆𝑣𝑎𝑝𝐻𝑚 𝑇 = 41 kJ/mol）- 在海平面高度(z=0)：T0 = 373K = 100°C = Tvap(P0)，其中P0 = 1 atm = 1.013 bar

• 我们寻找在海拔高度z1 = 2000 m处的T1 = Tvap(P1)，使用大气层等温模型作为理想气体： 结论： 热功率Pth与Tvap(z) - Tambiante(z) = Tvap(z) - T0成比例，随着z的增加而减小。因此，∆𝑡𝑐𝑢𝑖𝑠𝑠𝑜𝑛 = 𝐸𝑐𝑢𝑖𝑠𝑠𝑜𝑛/ Pth随着z的增加而增加：在高海拔地区烹饪时间更长！

第5章：热机

I. 循环热机

循环热机是一种包含热力学系统（通常是流体）和经历循环变化的机构的装置。在第I部分和第II部分，我们研究的是闭合系统的机器：相同的分子经历一个循环。 流体（就像机构一样）总是回到它的初始状态。

  1. 引擎/接收器 在一个循环过程中，系统以热能或机械能的形式接收或提供能量： • 引擎：W ≤ 0，向外界提供功 • 接收器：W ≥ 0 当它们提供非自发热传递时很有意义。 例如：从冷源取热能（"制冷机"）或向热源提供能量（"热泵"）。 任何状态变量X只取决于系统的状态，因此： 根据第一定律：根据第二定律：

  2. 单温循环机器 当一个热机在循环过程中接收的热传递来自一个标有温度T0的单一恒温器时，它被称为单温热机。 因此， 使用单温循环无法实现引擎。 备注：这是第二定律的历史表述之一，由开尔文勋爵提出。

  3. 多温循环机器 当一个热机在循环过程中接收的热传递来自多个标有温度Ti的恒温器时，它被称为多温热机。 我们得到了Clausius不等式： 其中等号成立的情况对应可逆变换。

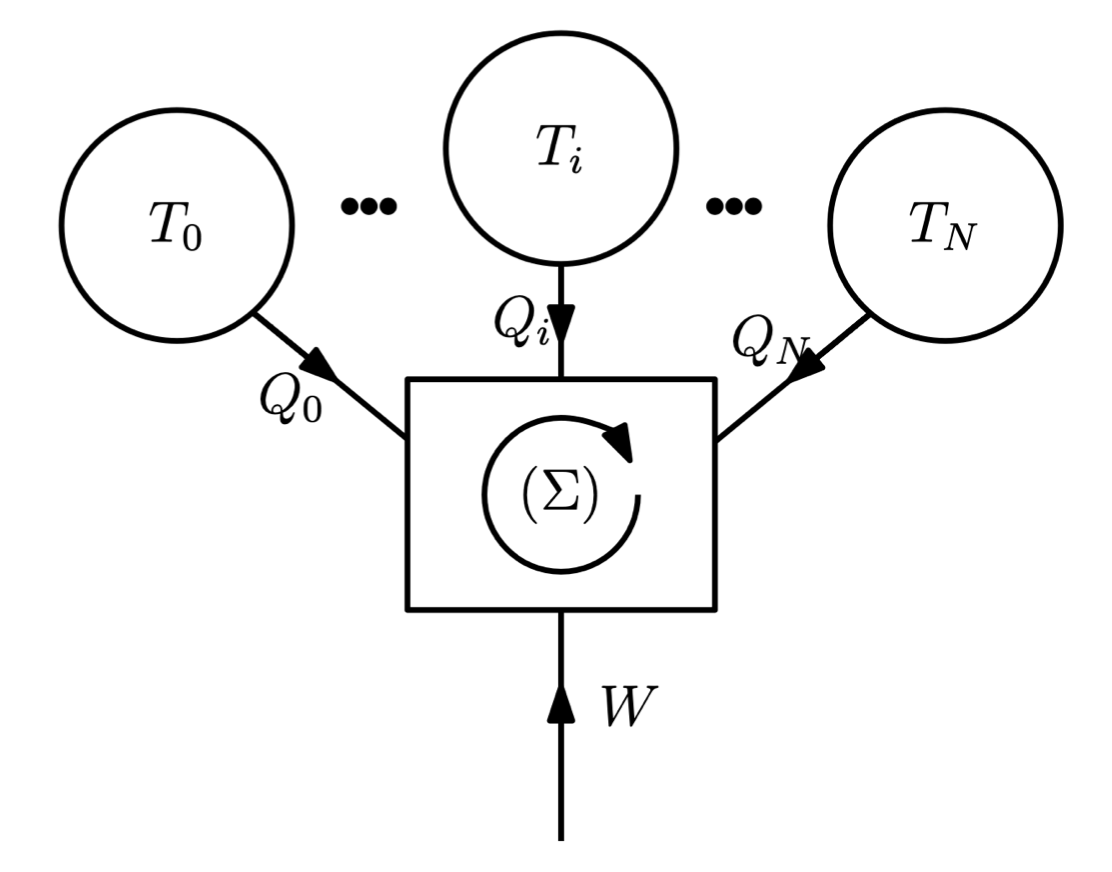
image-20231128215025870

II. 双温热机

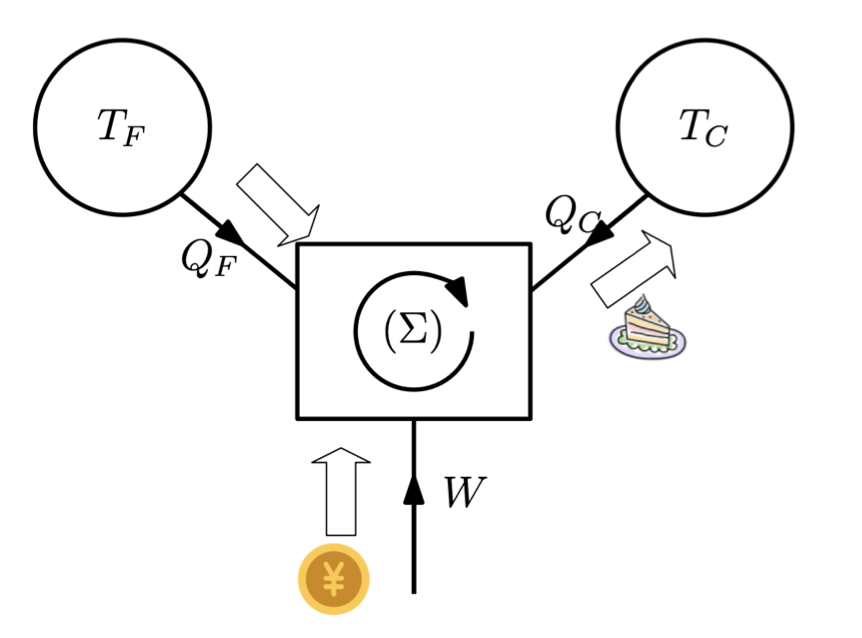
在双温循环热机中，系统从两个恒温器接收热能： • 高温源，温度为TC，在一个循环过程中向系统提供热量QC • 低温源，温度为TF（≤ TC），在一个循环过程中向系统提供热量QF

  1. Raveau图 Clausius不等式可表示为QC ≤ -TC / TF QF。我们要确定W=-QC-QF的符号。 我们可以区分出4个运行区域：

• 1: • 2: 不具有兴趣，因为它可以自发发生（W = 0）。

• 3: 不具有兴趣，因为它类似于单温热机。

• 4: 如果目标是QC ≤ 0: "热泵" 例如：将已经温暖的房屋加热（外部寒冷）。 如果目标是QF ≥ 0: "制冷机" 例如：将已经冷却的冰箱冷却（外部炎热）。

  1. 热力学效率
  1. 一般情况 效率被定义为想要的能量付出的能量；我们将理论最大效率表示为eth,max。 效率通常用表示，取值范围在0到1之间。
  2. 引擎的情况 我们支付QC≥0。我们希望W≤0。 例如：我们支付汽油（其燃烧）使汽车前进。

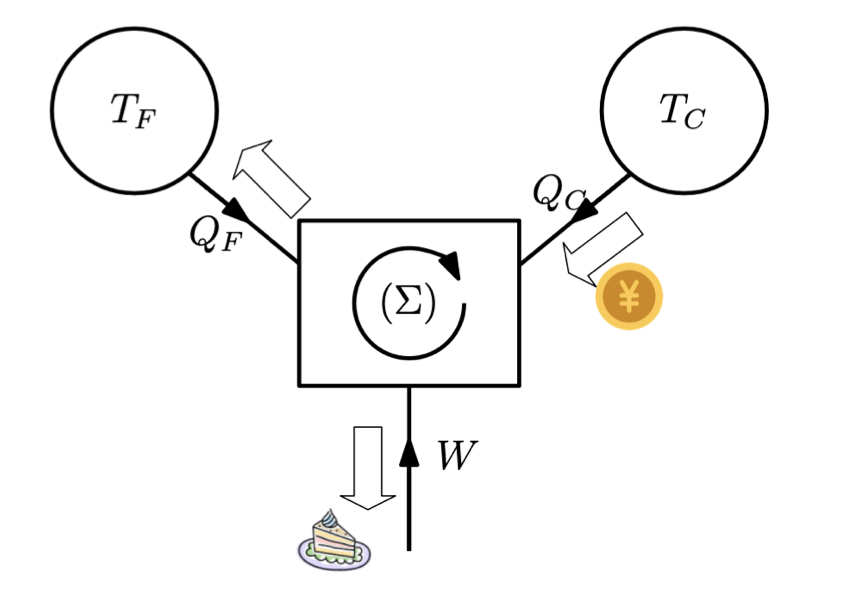
image-20231128215403214

  1. 制冷机的情况 制冷机接收一定的功来从冷源（容器内部）提取热能，并将热能传递给热源（外部环境）。 例如：冰箱和空调保持一个冷的容器。 为了保持恒定的TF，必须不断从容器中移除它从外界接收到的热能。在稳态下，内部的行为类似于一个冷源。 我们支付W≥0，我们希望QF≥0（电费账单）。

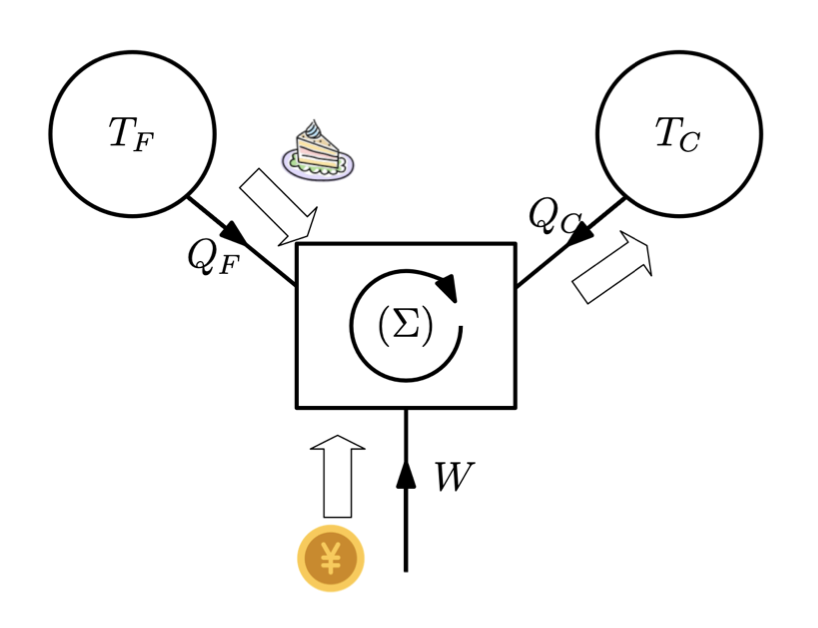
image-20231128215658902

  1. 热泵的情况 与制冷机的原理相同，但目标是从冷源中提取热量并将其传递给热源。 例如：冷气机在冬季的“加热模式”下加热建筑物内部。 我们支付W≥0，我们希望QC≤0（电费账单）。 image-20231128215747832
  1. 卡诺循环
  1. 定义 前面提到的效率在可逆循环中达到最大值。 实际上，存在一种唯一的可逆双温循环，即卡诺循环，其中： • 在与冷源进行热传递时，温度为TF • 在与热源进行热传递时，温度为TC 以避免由于T的不均匀性（系统的温度）而引起的不可逆性 • 循环的其余部分必须是可逆绝热的，即等熵的。 该循环包含两个等温过程，并通过两个等熵过程闭合。 卡诺循环是一个理想的循环，它是无限长的，因此在实践中无法实现。

图 TS 备注：与 PV 图中一样，该循环对于发动机来说是顺时针方向的。 GP 的瓦特图

  1. 具有可变温度源的机器 在时间的推移中，TC或TF可以变化，相应的源被称为伪热力学系统。我们以长时间打开后在t = 0时关闭的冰箱为例进行研究。 所研究的系统是经历循环的机器中的流体。 第一个假设：TF(t)在机器的循环中会发生变化，其中TF(t=0) = T0且TC = T0。 我们要找到以下内容： • 为了使TF < T1（其中T1 < T0），需要提供的最小功率Wmin(T1) • TF(t)的规律，特别是降低TF所需的时间 这是一个有趣的问题，没有课堂上的结果需要知道，这是一个很好的练习题目！

  2. 一个真实发动机的例子:Beau de Rochas 和 Otto 的四冲程循环

装备在大多数汽油汽车上的四冲程内燃机的工作原理:

image-20231129193646090

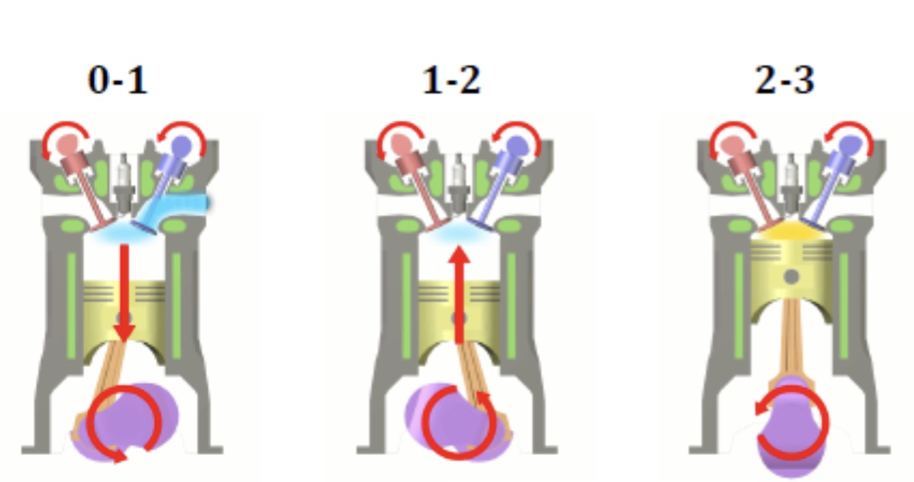
image-20231129193827725image-20231129194132250

0-1: 进气等压空气燃料混合气

1-2: 压缩可逆绝热

2-3: 燃烧等容(与高温源接触)

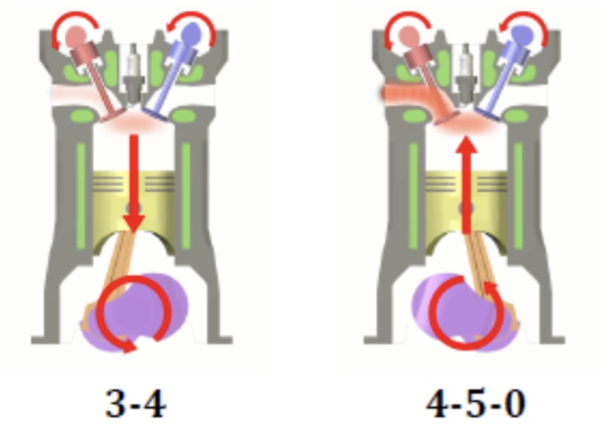
3-4: 爆炸/膨胀可逆绝热

4-1: 排气等容燃烧气体,流体(与低温源接触)

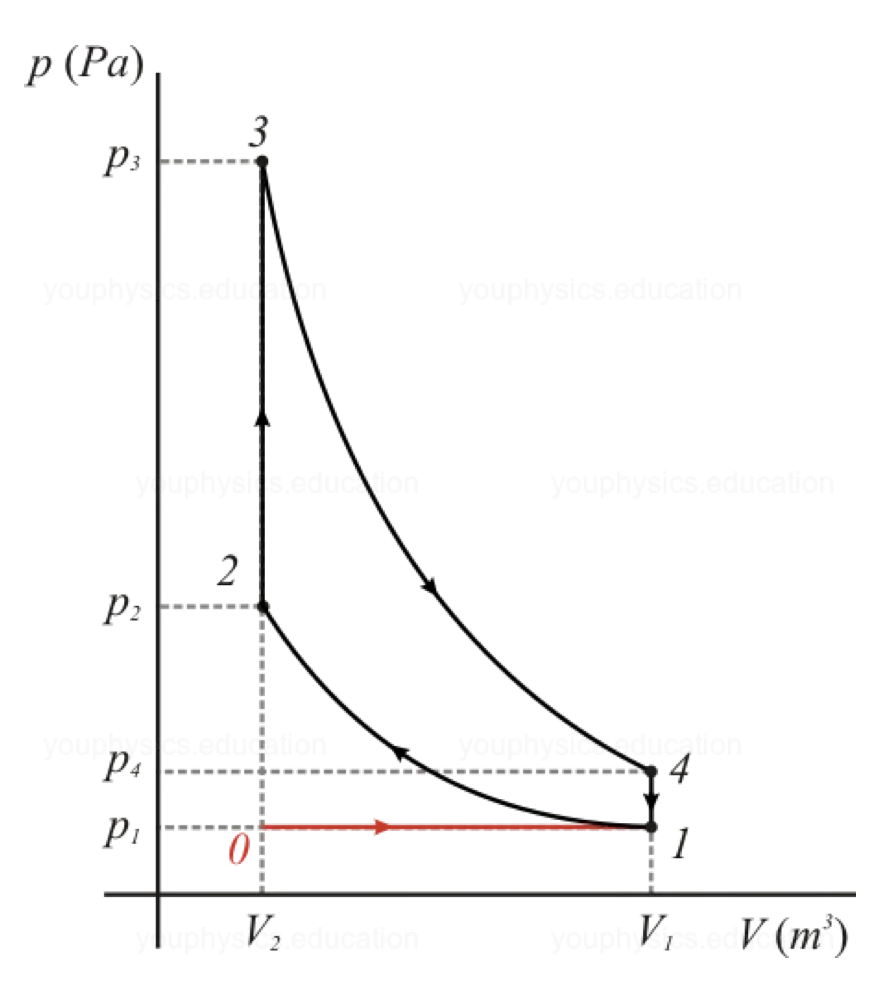
理想情况下

image-20231129194204808

• 热源提供的热量传递:汽油(为简化由碳氢烃组成)的燃烧化学方程式简化:

CnH2n+2 + (3n+1)/2 O2 = n CO2 + (n+1) H2O 而∆化学焓=-44 MJ/kg

∆化学焓描述了反应体系接收的焓。这里∆化学焓< 0:所以反应会向外界提供能量,即反应是放热的(如果∆化学焓> 0则反应是吸热的)。

对于质量为_m_ 的CnH2n+2,

• 练习:在假设循环近似静态和混合物为理想气体的条件下,计算Beau de Rochas循环的最大效率eBDR max。

我们计算得出eBDR max ≃ 0.6,但对于实际发动机:eBDR 实际 ≃ 0.5,所以η = eBDR 实际 /eBDR max ≃ 85%。柴油发动机由另一个循环描述:e 柴油实际 ≃ 0.4 < eBDR 实际。效率是选择发动机的一个标准,但功率和技术限制也很重要。我们需要做出折衷:尽管柴油发动机的效率更低,但仍然经常使用柴油发动机。

III. 流动流体装置

我们之前考虑的机器由流体组成,其所有粒子同时经历相同的变化。但在实际情况下,这并不总是正确的,流体中不同部分的粒子在 流动 时可以同时经历不同的变化。

我们可以隔离出其中一个部分,它会依次经历这些变化。

  1. 概述

a)描述

流体进出机器,构成开放系统,与外界交换物质。在通过机器的过程中,流体从外界(温度为Text)接收了能量:

  • Pth为热功率。

  • Pu为机械功率(有效功率,称为“指示功率”),来自机器运动部件。

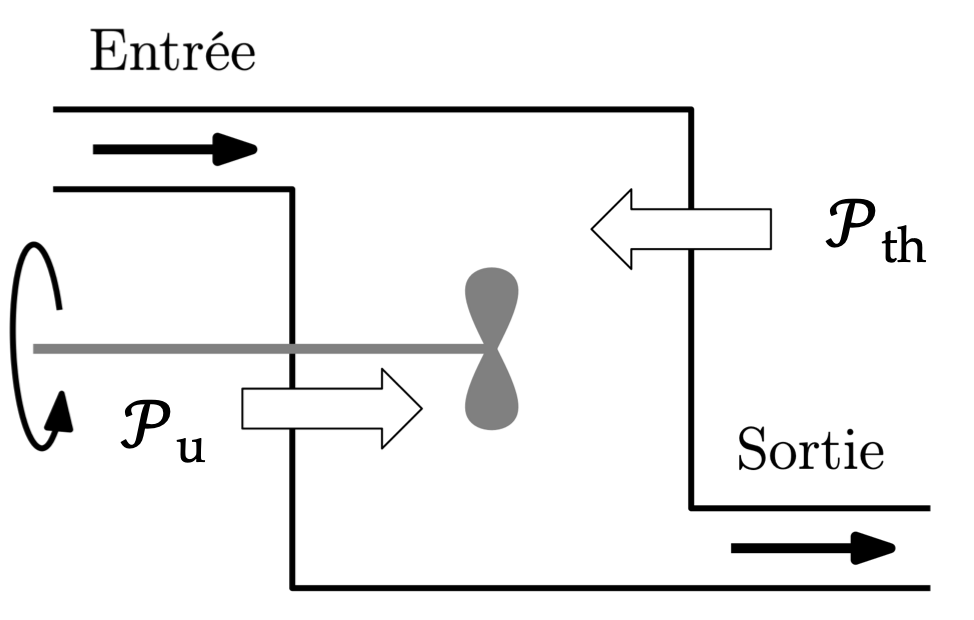
image-20231129194647958

我们假设整个系统以稳态工作:

功率恒定,单位时间通过系统的质量也恒定。

b)研究系统

之前看到的热力学原理只适用于封闭系统。因此,我们需要在时刻t和t + dt之间构建一个封闭的系统∑:

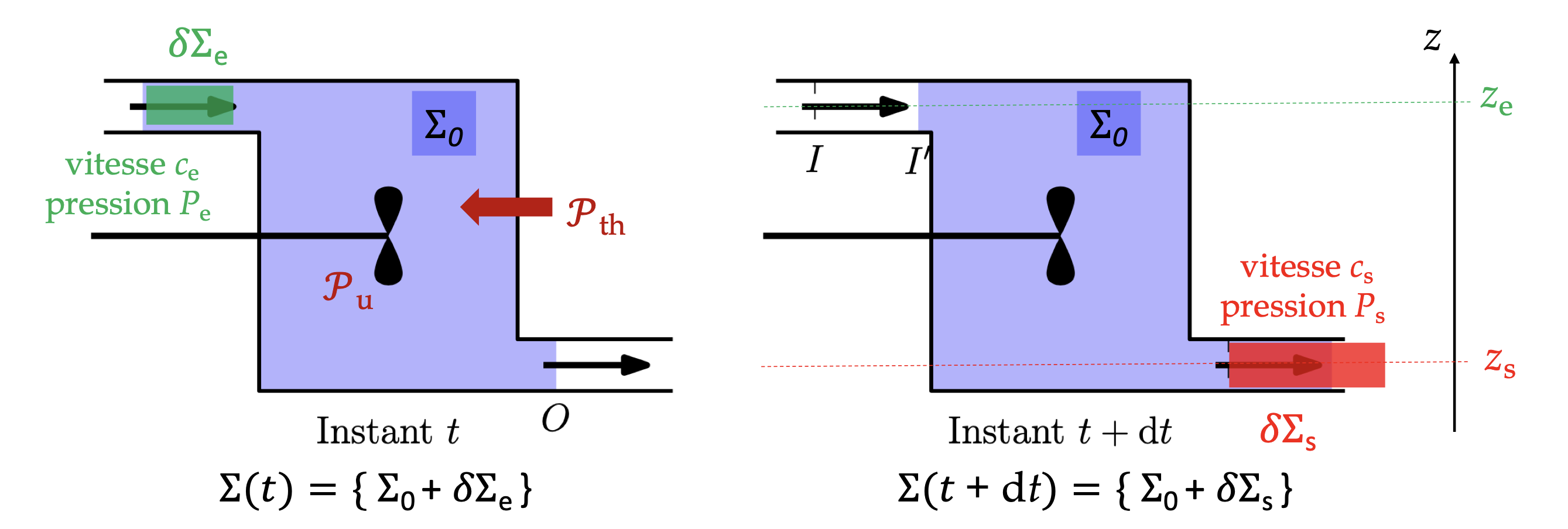
image-20231129194953917

c) 质量平衡

我们定义m0为Σ0的质量,δme为δΣe的质量,δms为δΣs的质量。系统Σ是封闭的,所以其质量不变: 然而在稳态条件下(RP):

我们可以推导出质量流率 Dm 在稳态条件下保持恒定:

注意:

  • DV体积流率在相变的情况下不是先验恒定的。

  • 在后续部分,我们关心的是入口和出口参数的变化,而不是平衡状态之间的变化(比如由第一定律给出的)。

  1. 能量交换:开放系统第一定律(PPSO)

我们定义Σ的能量为_E_:其在_t_和_t+_d_t_之间的变化量为:

根据第一定律:

  1. 质量比熵平衡

我们定义出口和入口的质量比熵为ss 和 se,单位为J/K/kg。我们定义生成的质量比熵为s̃e(≠ se)。

根据第二定律:

回顾不可逆的典型原因:

主要是温度的非均匀性和黏性摩擦。如果定义熵生成率或熵功率为σ:

  1. 第一个例子:焦耳-汤姆森膨胀

假设:

• 稳态问题

• 通过绝热器缓慢流动(Pe、Ps 、ce和cs明确定义为较小值)

根据PPSO,

如果忽略ec的变化,我们可以重新获得这个膨胀的绝焓性质:

我们也有: 如果气体是理想气体,Ts = Te,则

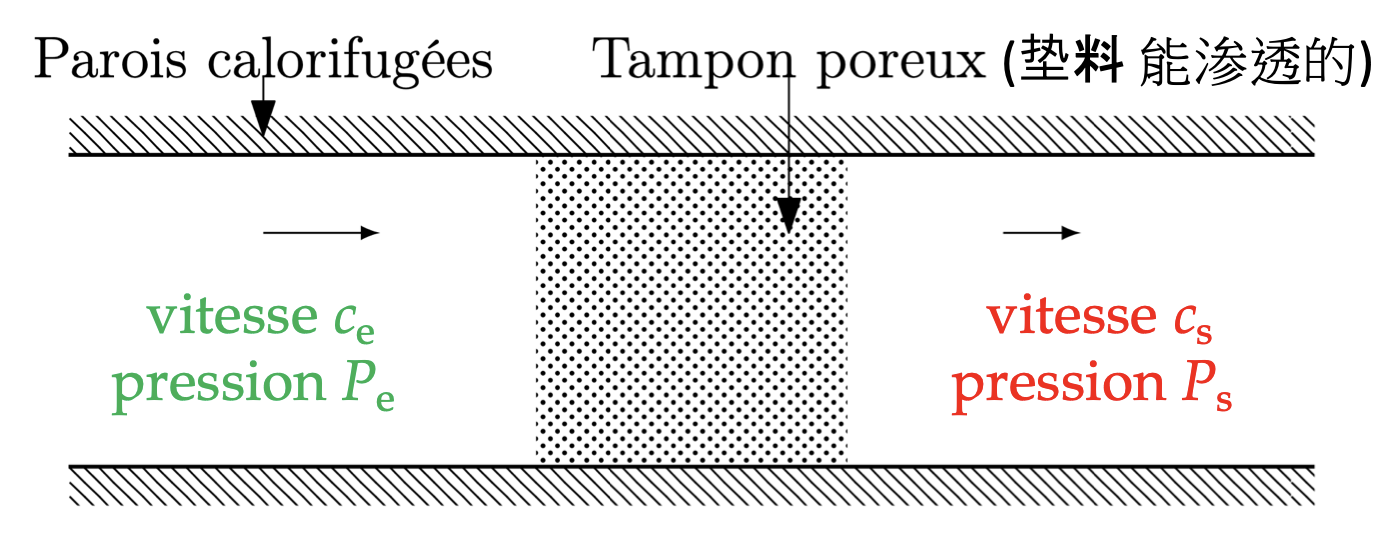
image-20231129195552063

Parois calorifugées: 绝热壁

技术应用:

制冷机的膨胀装置(也用于潜水等)。Ph图(即制冷技师图)比较适用:

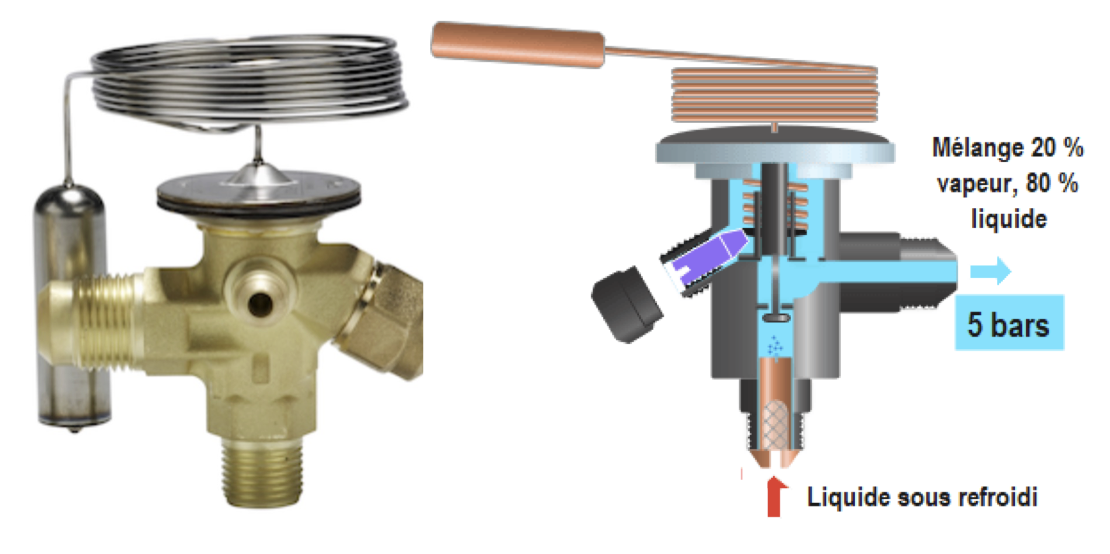
image-20231129195646735

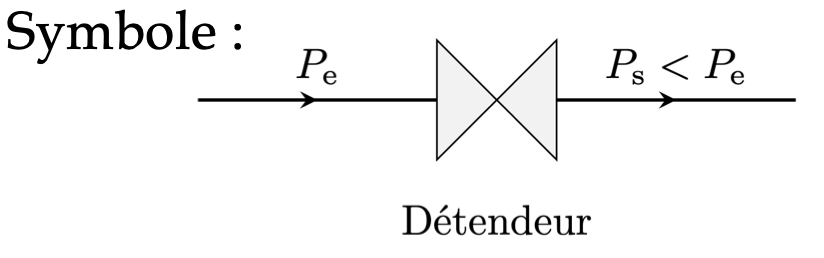
符号: image-20231129195738082

Détendeur : 膨胀阀

  1. 第二个例子:空气源热泵

a)原理

它用于将房屋散热器中的供暖水加热到35°C(热源,QC<0),其能量来自室外5.0°C的空气(冷源,QF>0)。

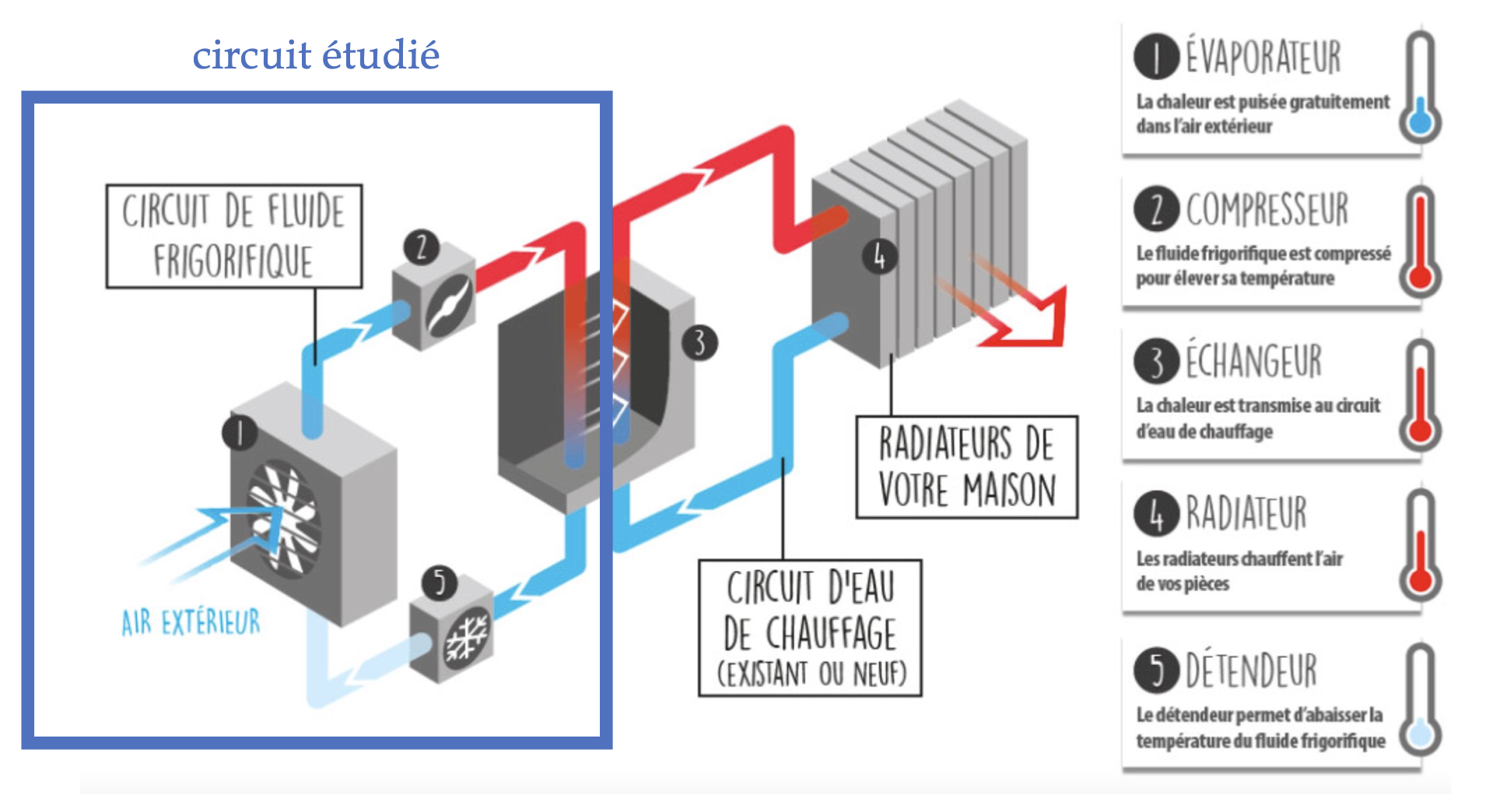
image-20231129195851553

b)循环变化

与冷源和热源接触时会发生状态变化,因为交换的能量比仅仅温度变化的情况下更多。

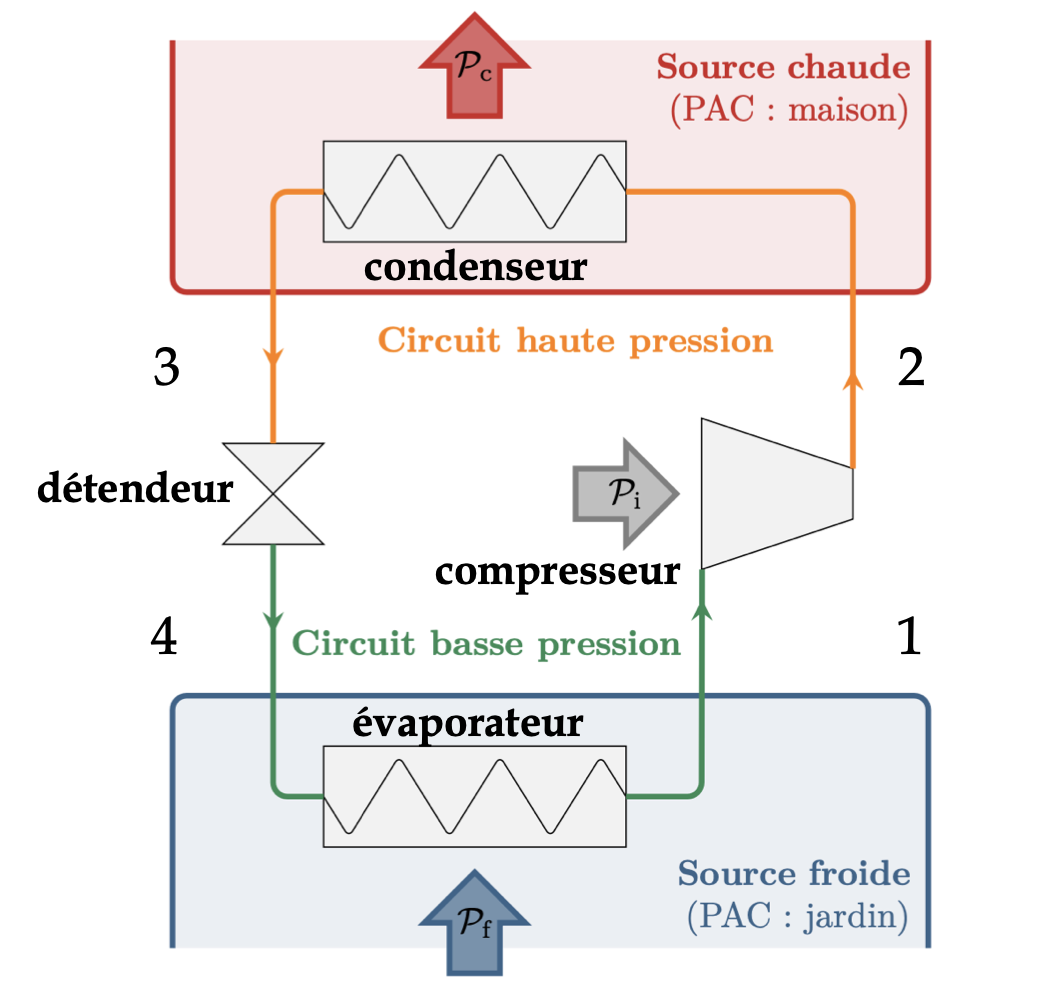
image-20231129200025457

1-2: 流体气体的压缩,P 和因此T 增加(例如 T>TC)。

2-3: 流体气体的液化,QC<0 因为 ∆liqHm<0。

3-4: 流体液体的膨胀,P和因此T降低(例如T<TF)。

4-1: 流体液体的汽化,QF>0因为∆vapHm>0。

c)制冷技师图

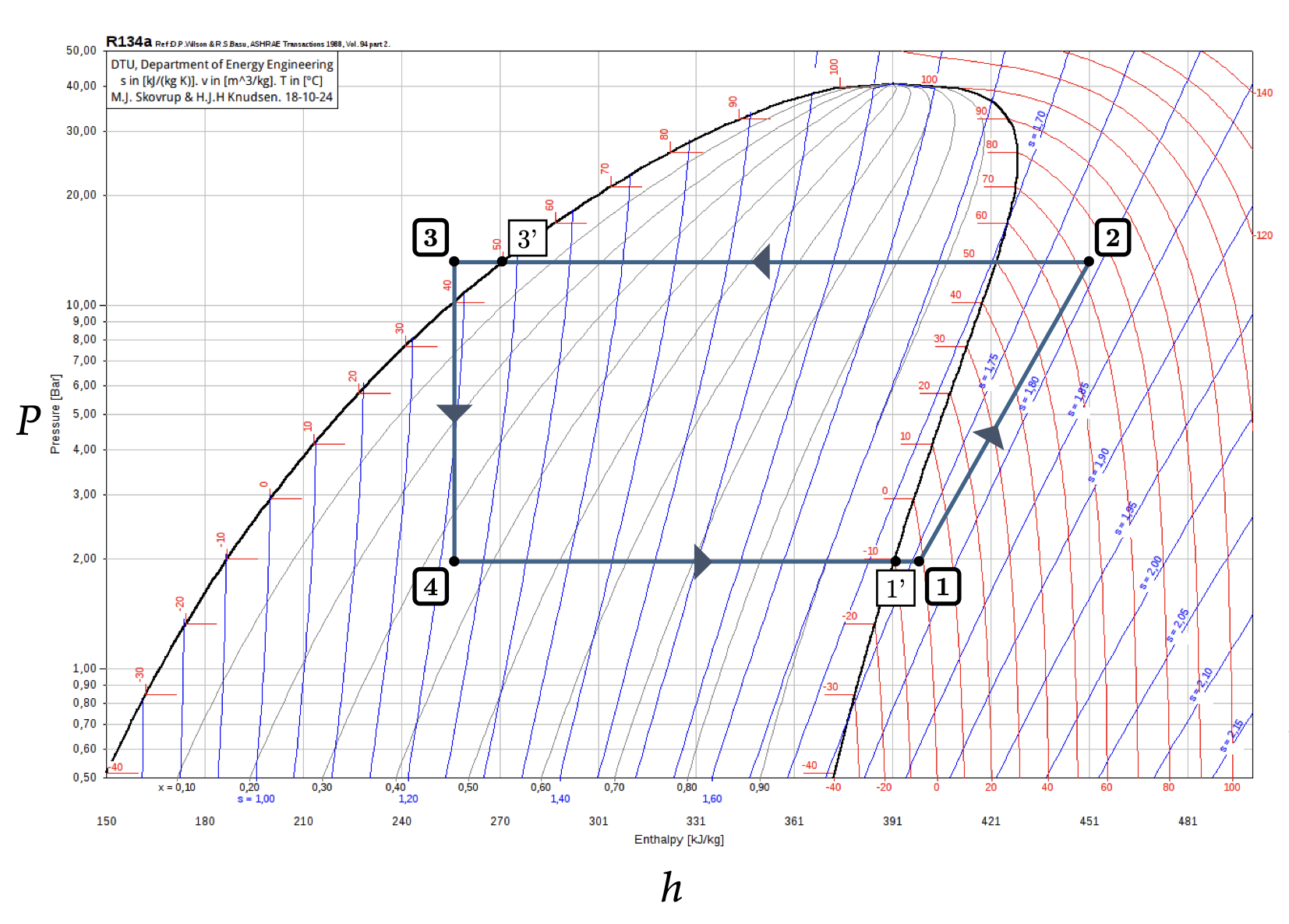
image-20231129200312748

吸热循环顺时针运行:

1-2:气体流体压缩, P 和因此T增加(例如T>TC)。Wu = W12>0 无论熵不变量!

2-3:气体流体液化,QC<0。等压(高压)过程,∆liq h<0。

3-4:液体流体膨胀,P和因此T降低(例如T<TF)。 焦耳-汤姆森绝焓膨胀。

4-1:液体流体汽化,QF>0。等压(低压)过程,∆vap h>0。

d)效率

定义:与热源接触:

接收的功:对于理想的卡诺循环,我们有:第5章小结

第5章小结

要求的技能:

  • 使用两个原理分析循环机器
  • 卡诺理想循环用于热机
  • 计算效率和效益
  • 在PV图中描述一个循环
  • 读取制冷技师图以分析流动流体